БИОМЕХАНИКА ПЕРЕМЕСТИТЕЛЬНЫХ ДЕЙСТВИЙ И ПРЫЖКОВ.
1.
Метание гранаты.
2. Прыжки.
3. Прыжки в
высоту.
4. Прыжки в
длину с разбега.
Состязание
в метаниях и прыжках были популярны всегда. Ведь от умения далеко и точно
метать, далеко и высоко прыгать нередко зависит жизнь человека.
В Древней
Греции метали диск и копье. Состязания в метании копья на дальность и на
точность производились между ассирийскими солдатами. В Ирландии на народных
празднествах особой популярностью пользовались прыжки в высоту и вид
метаний, который послужил прообразом будущего метания молота. Прыжок в
высоту для воинов Севера был обязательным. Чтобы быть допущенным в ряды воинов,
нужно было уметь перепрыгнуть через стоящего человека.
1. МЕТАНИЕ
ГРАНАТЫ.
Для всех
разновидностей метаний характерны общие закономерности. Но детали техники
в разных видах метаний различны. Метание гранаты с разбега:
- разбег;
-
подготовка к броску;
- бросок;
- остановка
после броска.
Отметим,
что скорость снаряда во время броска должна непрерывно нарастать.
Необходимо
постепенное вовлечение в процесс метания звеньев руки - от проксимальных к дистальным.
Непосредственно
перед броском тело метателя приобретает форму как бы натянутого лука.
Угол вылета
снаряда должен быть меньше (30-40°). Дальность полета снаряда при оптимальном
угле вылета определяется в основном скоростью вылета. Поэтому следует
организовать свои двигательные действия так, чтобы максимально увеличить
скорость вылета.
При метании
мяча в цель точность попадания тем выше, чем меньше дальность:
1 м -
40-80% попадания
7 м -
10-20% попадания.

Полет тела,
брошенного под углом к горизонту:
а – точка вылета, б – точка
приземления, α – угол вылета, v0 – начальная скорость полета, v1 – горизонтальная составляющая скорости полета, v2 – вертикальная составляющая скорости полета, S – дальность полета, H – высота полета

Метание мяча в
цель:
1 – момент
вылета мяча и попадания в цель (обозначены стрелками): 2, 3 и 4 – акселерограммы дистальной части плеча, предплечья и кисти
(по А. А. Данилову, переработано)
Есть
основания ожидать, что если человек точен в одном виде метаний, то он будет
точен и в других видах. При обучении прицельным метаниям нужно иметь в
виду существование сенситивного периода (от 12 до 14 лет), когда обучающие
мероприятия наиболее эффективны. В этот период происходит быстрое
естественное развитие меткости.
ЗАДАЧА.
Диск в
начале броска делает 500 оборотов в 1 мин. Его момент инерции относительно
вертикальной оси равен J = 0,00148 кг м/сек2.
НАЙТИ.
Кинематическую
энергию диска (Ек).
РЕШЕНИЕ.
Известно,
что угловая скорость диска равна:

Кинетическая
энергия определяется по формуле:
Ek
= 
ЗАДАЧА.
Копье
брошено с начальной скоростью V = 24,0 м/сек под углом α
= 45° к горизонту.
НАЙТИ:
-
дальность полета (S);
-
длительность полета (t);
-
максимальную высоту полета (Нмах);
-
скорость в момент, когда копье достигает (Нмах) и при
приземлении (V).
РЕШЕНИЕ.
1 . Зная
вектор скорости и угол α = 45°, можно найти его
составляющие по осям (X и У)
Vx = Vy
V = ![]()
Vx=Vy=![]()
2.
Определим дальность полета (S):
 ;
;
3.
Длительность полета (t) можно определить из формулы:
S = Vt
 ;
;
4.
Максимальная высота полета определяется по формуле:
 .
.
5.
Горизонтальная скорость копья в продолжение полета остается постоянной Vх = const = 17.0 м/сек. Вертикальная скорость копья в момент
достижения (Нмах) равна нулю. Скорость при
приземлении равна начальной скорости вылета и составляет: 24,0 м/сек.
ЗАДАЧА.
Мяч
подброшен вертикально вверх с начальной скоростью Vo = 29,4 м/сек
НАЙТИ:
-
максимальную высоту перемещения мяча (Нмах);
-
скорость мяча на высоте (h = 10.0 м);
-
скорость (V) мяча в момент времени (t1 = 2,0 сек);
- высоту
(Н) в момент времени (t2 = 4,0 сек);
- время
полета мяча (tпол.)
РЕШЕНИЕ.
1.
Кинетическая энергия, затраченная на сообщение скорости мячу, равна по
перемещению мяча в поле силы тяжести:
 ,
,
Преобразуем
формулу с учетом того, что (V) на высоте (Нmах) равна нулю, получим:
 .
.
2. Применяя указанную выше формулу о
кинетической энергии, определим скорость мяча на высоте h = 10.0 м, получим:
![]()
3. Скорость
подъема мяча через t1 =
2.0 сек находится по формуле и будет равна:
V = V0 - gt (V = 29.4 - 9.8 х 2.0 = 9.8 м/сек).
4. Высота перемещения мяча через t2 = 4.0 сек находится по формуле и
будет равна:

5. Когда
скорость мяча уменьшится до нуля, мяч достигнет самой высокой точки своего
подъема:
- tвзл. - есть
время подъема;
- tпол. = tвзл. + tпад.
- V = V0 - gtвзл. = 0

tпол. = 
2. ПРЫЖКИ
Исходя из
подготовительной фазы прыжка, можно выделить прыжки с места и прыжки с разбега.
Отталкивание при прыжках производится одной или двумя ногами. По условиям
полета прыжки бывают простые (со свободным полетом) и опорные, при которых
часть полета совершается с опорой руками на снаряд. Приземление может
совершаться на обе ноги одновременно, на одну ногу, на руки, на ногу и руки
одновременно.
Прыжок с
отталкиванием одной ногой и с приземлением на толчковую ногу называется
скачком, а с приземлением на маховую ногу - прыжком "шагом".
Под
действием силы тяжести тело движется прямолинейно, вертикально вниз и
равноускоренно (с ускорением 9,81 см/сек).
Угол, образуемый горизонталью с направлением отталкивания,
называется углом отталкивания, а угол между горизонталью и направлением
полета - углом вылета. Угол вылета меньше, чем выше скорость разбега. Угол
вылета для максимальной дальности полета теоретически должен быть равен 45°.
При прыжках в длину с места он близок к этой величине. При прыжках в длину с
разбега угол вылета в 45° может иметь место только в том случае, если
вертикальная составляющая, скорость от толчка и скорость oт разбега будут
равны между собой, или первая будет больше второй (при угле отталкивания меньше
90°). Фактически же при прыжках в длину с разбега имеется обратное
соотношение, т.е. скорость от разбега значительно больше скорости от
толчка, и поэтому угол вылета обычно не превышает 20-25°.
При прыжках и высоту угол вылета достигает 60-75°. Он обусловлен
соответствующим соотношением составляющих скоростей - сравнительно небольшой
скоростью от разбега и высокой скоростью от толчка.


Формы траектории о.ц.т.т.
при различных прыжках:
а – в длину, б – через высоту,
в – на высоту, г – в глубину

Углы вылета при прыжке:
а – в длину с разбега, б – в высоту с разбега
3. ПРЫЖКИ В ВЫСОТУ.
Прыжок состоит из разбега, отталкивания, перехода через планку
и приземления.
При прыжке способом "перешагивание", или
"ножницы", прыжок выполняется под углом 30-45°. Отталкивается
спортсмен дальней от планки ногой в 70-80 см от проекции планки.
Основной недостаток этого прыжка чрезвычайно высокое положение
общего центра масс тела по отношению к планке в момент перехода через нее.

При прыжке способом "перекат" этот недостаток частично
устраняется. Разбег происходит под углом 30-40° к планке, отталкивание
выполняется ближней к планке ногой.
В еще более рациональном способе прыжка в высоту - "перекидным"
- разбег, подготовка к отталкиванию и отталкивание выполняются так же, как и в
способе "перекат". Однако переход планки происходит в положении лицом
вниз.
Мировой рекорд в прыжках высоту у мужчин
перешагнул за 2 м 40 см, а у женщин - за 2 м.
Спортсмены используют - "перекидной" и "фосбюри-флоп" (спиной вниз).
У взрослых прыгунов вертикальная составляющая силы действия на
опору при отталкивании составляет 3500-6000 Н. Эти величины
увеличиваются с ростом подготовленности прыгунов. Значительную роль
в этом играют вертикальные ускорения маховых конечностей. Задача оптимизации
состоит в том, чтобы увеличить импульс силы, несмотря на снижение длительности
отталкивания.

Прыжок в высоту способом
«перешагивание» (вверху) и «перекидной»

Прыжок в высоту способом
«перекат» (слева) и «перекидной»
Н1
– высота общего центра масс; Н2 – высота подъема общего
центра масс; Н3 – разница между высотой общего центра масс
тела при переходе через планку и высотой планки
4. ПРЫЖКИ В ДЛИНУ С РАЗБЕГА.
Результат
прыжка сильно зависит от скорости в завершающей части разбега. Характерной
особенностью техники разбега является увеличение времени контакта с опорой и
резкое уменьшение времени полета в последнем шаге разбега. Этим создаются
предпосылки для быстрой и точной постановки ноги на брусок и активного
отталкивания. Если время контакта с опорой при отталкивании меньше, то
прыжок длиннее. Чтобы эффективно оттолкнуться, надо быстро поставить ногу
на брусок и стремительно подбросить себя вперед вверх. В момент отталкивания
важно как можно быстрее пройти вперед через опорную ногу, направляя грудь
и плечи вверх.
Способ
"согнувшись".
Способ
"прогнувшись".
Способ
"ножницы".

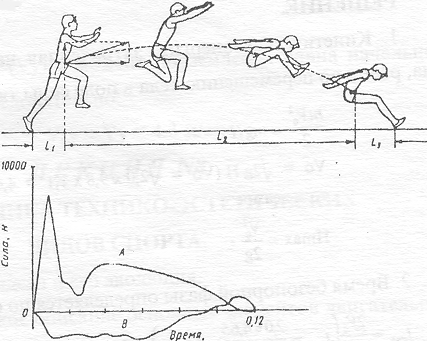
Изменение во
времени силы действия прыгуна на планку при отталкивании: А –
вертикальная составляющая; В – горизонтальная составляющая (по Bosco с соавт.);
кинематика прыжка в длину способом «согнувшись»: стрелками
обозначены векторы скорости общего центра масс в начале полета; время в
секундах (по В. А. Петрову, Ю. А. Гагину)
В последние
3-4 шага перед отталкиванием спортсмен приводит туловище в положение,
близкое к вертикальному и снижает высоту общего центра
масс тела. Эти изменения положения тела сопровождаются удлинением
предпоследнего шага и соответствующим укорочением последнего.
Назначение
отталкивания - сообщить телу вертикальную скорость, сохраняя как можно большую
горизонтальную скорость.
Спортсмен
должен стараться в момент приземления выставить стопы как можно дальше от
центра массы тела.
ЗАДАЧА:
При
прыжке В.Брумеля в высоту с разбега (результат 2,28 м) ОЦТ прыгуна был поднят
на Н = 1,1 м.
НАЙТИ:
-
вертикальную скорость взлета (Vo);
- время безопорной фазы (tпол.).
РЕШЕНИЕ.
1. Кинетическая
энергия, затраченная на сообщение скорости тела, равна по перемещению тела в
поле силы тяжести:

Vo = ![]()
то же
самое:

2. Время безопорной фазы определяется по формуле:

ЗАДАЧА.
На
Олимпийских играх в Мехико Б.Бимон в прыжках в длину
с разбега показал результат S = 8,9 м. Длительность прыжка составила tпол. = 0,9 сек.
НАЙТИ:
- горизонтальную и вертикальную составляющие
начальной скорости вылета (Vx и Vy);
-
максимальную высоту (Н) ОЦТ спортсмена в безопорной
фазе.
РЕШЕНИЕ.
1.
Горизонтальная скорость тела:

2. С момента достижения спортсменом максимальной
высоты (Н) движение ОЦТ является равномерно-ускоренным. При этом начальная
скорость равна нулю, а ускорение равно (g). Такое движение описывается формулами
свободного падения тела:
Vy = gt = ![]() (Vy = 9,8 x 0,45 = 4,3 м/сек).
(Vy = 9,8 x 0,45 = 4,3 м/сек).
 ,
,
где ![]()
Так как
скорость (Vy) в момент приземления равна начальной скорости вылета, то,
следовательно:
V0y = Vy = 4.3 м/сек.